We have a hyperbola in the form  . . It's center is at (h, k), or (-6, 6). The values a and b, which will be very helpful for finding everything else, are 4 and 6, respectively. Remember, a always hangs with x, and b is always under y. Which one is positive or negative doesn't change that a bit. Hyperbolas have two vertices, and their locations depend on if it is a vertical or horizontal hyperbola. And that depends on which variable is positive. Here, y is positive, so the graph will be vertical. The vertices will be above and below the center by b. That is, (-6, 6 ± 6) = (-6, 0) and (-6, 12). Let's nab the two asymptotes next. They are identical, except that the signs of their slopes are opposite. Their equations are  . . 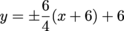
Be careful with h and k. We put -h next to x, but positive k outside the parentheses. 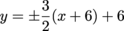
Last but probably not least are the foci. We've got an equation to find their distance from the center, and it is f2 = a2 + b2. Plugging in our values, we get: f2 = 16 + 36 = 52 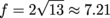
That's just the distance to the foci; we need to find their coordinates to finish the problem. They go in the same directions from the center as the vertices do, so they are above and below the as well. (-6, -1.21) and (-6, 13.21) We've finally found all the important parts of this hyperbola. |