Nuclear Physics
We've spent a great deal of time in this Atomic section discussing electrons and their orbits and their energies, but they're not the only particle in an atom. As we saw in Section 1, Ernest Rutherford discovered the nucleus in the early 20th century by going shooting—shooting α-particles, that is. Nuclear physicsrefers specifically to the physics of the nucleus.
Here's a puzzler: what holds the nucleus together?
Neutrons are neutral and protons are positively charged. The electric force can't act there. Mathematically, if we insert the neutron's charge into Coulomb's Law, we'll get a big fat zero. We have to consider the mutual repulsions of all the protons together in the nucleus for any Z > 1, as well.
"Mutual repulsion" because like charges repel each other. That means something must be missing here. What's this "nuclear glue" that keeps the nucleus together? Why would neutrons hang out with repulsive protons, anyway?
With James Chadwick's 1932 discovery of the neutron came another new concept: the nuclear force. It's a strong force that acts within the range of the nucleus, go figure. Since nucleons reside inside the nucleus, all nucleons feel the presence of the nuclear force.
Let's take a step back. Let's talk about forces. Charged particles, such as protons and electrons, feel the electromagnetic force. Nucleons, such as neutrons and protons, feel the nuclear force. And every particle in the universe feels the gravitational force. It's the relative strength of these forces at various distances that determine which force rules in a given situation. Gravity rules the movement of galaxies and solar systems, the electromagnetic force rules for electrons around a nucleus (and elsewhere), but the nuclear force rules the nucleus.
By continued scattering experiments, the size of the nucleus of an atom was determined to be roughly R = RoA1/3, where Ro = 1.2 fm, that's 1.2 × 10-15 m, and A is the mass number of the nucleus. This image of the Helium atom below gives us a good idea of the size of a nucleus in comparison with the size of an atom. The atom has much more empty space in it than scientists had originally conceived.
The word nucleus comes from Latin. It's short for nux, latin for kernel. Yep, eating popcorn at the movies has an entirely new meaning now, doesn't it?
The nuclear force is actually divided into two. We won't really get into the technical details here, but some particles only feel one kind or the other depending on their nature. These two sides of the nuclear force are called the strong force and the weak force. As its name implies, the weak force is weaker than the strong force. It's also weaker than the electromagnetic force, but still stronger than gravity.
The particles subject to the strong force are called hadrons and the particles that feel the weak force are called leptons. Both protons and neutrons are hadrons. Electrons, incidentally, are leptons, but they're not in the nucleus under ordinary circumstances so in a nuclear sense, we ignore the weak force.
If we inspect the ratio of protons to neutrons throughout the periodic table, we'll notice that the ratio changes.
The smaller atoms have about an equal number of protons and neutrons. Oxygen-16, for instance, has 8 protons, 8 neutrons. When we get to Scandium-45 , however, there appears to be a bit of a branch-off. Scandium has 21 protons, but 24 neutrons. This difference just keeps getting bigger as the sizes of nuclei grow. Why is that? To understand the answer to this question, let's first investigate the binding energy within a nucleus as a function of atomic mass A.
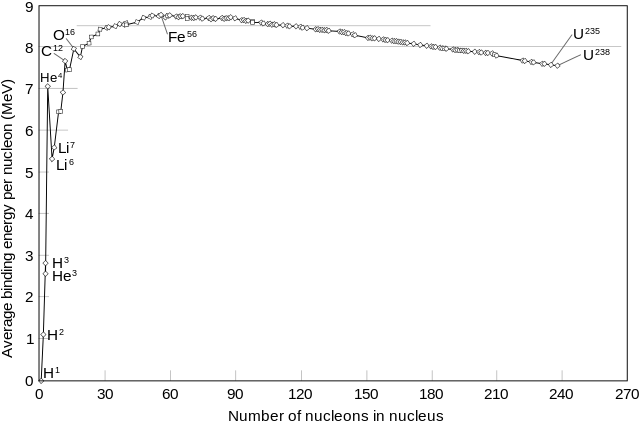
Although we won't discuss nuclear orbitals today (they're waaaay too complicated), just like electrons, nucleons have a binding energy that keeps them in the nucleus. The mass number is the mass of the nucleus. That nucleus contains neutrons and protons, and the binding energy, Eb, that binds them together. The graph above shows that Iron-56 has the highest binding energy per nucleon, granting it the most stable nucleus of all the elements and isotopes out there.
Albert Einstein showed that E = mc2 as we studied in Relativity. Let's apply this to the energy of a nucleus to find the binding energy within the nucleus, Eb.
In that case the total energy in there is E(nucleus) + Eb = E(neutrons) + E(protons). Solving for Eb, we get Eb = E(neutrons) + E(protons) − E(nucleus). Using E = mc2, and dividing out c2, we're left with mass only, such that M(binding) = M(neutrons) + M(protons) − M(nucleus).
The M(binding) here is just the mass associated with the mass energy, otherwise known as the mass defect, or how much the mass changes from E = mc2.
Let's review.
The atomic number is the number of protons, Z; the mass number is the number of nucleons, A. This means the number of neutrons N is simply given by N = A − Z. M(neutrons) is just the number of neutrons multiplied by the mass of 1 neutron, and
M(protons) is just the number of protons multiplied by the mass of 1 proton. Review's done; we're moving on.
Let's take
as an example from the Periodic Table. Why does oxygen-16 get to be the cool isotope of Oxygen?
There are two reasons why Mr. Sixteen is so important. The first reason is pretty straightforward. It's the most naturally abundant on the planet, at 99.6% of all the naturally-occurring Oxygen on Earth. If we took a sample of 1000 random Oxygen atoms, we'd get about 996 Oxygen-16 atoms.
There's one more reason, related to the first. Oxygen-16, Oxygen-17, and Oxygen-18, are stable isotopes. This means they will stay as is, not emitting radiation to turn into something else like an unstable isotope would.
Stable isotopes are naturally abundant for a reason: they don't change into something else. So of course unstable isotopes of any element aren't naturally abundant: the nucleus is too prone to change for that to happen.
Radioactivity was discovered by Henri Becquerel in 1896. One day, he noticed that the some photographic film he developed turned out foggy. When he looked into what happened to the film, he realized that the film had been left besides some uranium compounds. He figured the "fogginess" was due to something the uranium was emitting. He was spot on.
We've mentioned radiation before when we studied electromagnetism. Cherenkov radiation and Bremsstrahlung radiation, for instance, are examples of radiation emitted as photons, or light.
The Polish doctoral student Marie Curie followed Beckerel's footsteps with her husband Pierre. Together, Marie and Pierre discovered other radioactive substances. They discovered Thorium, Radium, and Polonium, which Marie Curie named after her native country, Poland. The Curies won the Nobel Prize in 1903 with Becquerel.
The Curie couple discovered three types of emissions: alpha, beta, and gamma radiation. In other words, an unstable isotope spontaneously decays into another element while emitting one (or more) of those three particles from its nucleus. We've encountered α-particles before: they're what Rutherford used in his experiment that led to the discovery of the nucleus.
Once again, alpha particles are Helium nuclei with 2 neutrons and 2 protons. Since there are no electrons in nuclei, an α-particle carries a net +2 charge. The beta particles in β-radiation, on the hand, are electrons. Both α and β particles belong to a class of corpuscular radiation because they have mass, although α-particles, being heavier than electrons, don't travel very far through a material before they lose energy from collisions and stop.
The most powerful and potentially harmful source of radiation comes from gamma-rays, γ-rays. These are photons of the highest energies and frequencies possible in the electromagnetic spectrum, above 100 keV. We also call them "penetrating radiation" because gamma radiation, unlike alpha and beta radiation, can travel through skin. x-rays are penetrating radiation too (there'd be no picture of bones if the x-rays didn't penetrate), which also makes them dangerous.
through.
Any kind of radiation is bad for organisms, as we've all heard by now. Crossing paths with alpha, beta, and gamma radiation causes damage to tissue. Frequent, repeated exposure can lead to cell mutation, which turns into cancer. And that is why we always wear sunscreen, that's right, even the lower energy radiation from the sun's ultraviolet light over time can cause cancer. Radiation is what makes atomic weapons so terrible. It's not just the impact of the explosion itself that cause horrors, but the awful side-effects of alpha, beta, and especially gamma radiation too.
At what rate is this nefarious radiation emitted?
It depends on the isotope and how much of the isotope there is. Each isotope has a mean lifetime τ, pronounced tau. It's the average time a radioactive particle lives before it decays into something else emitting a type of radioactive particle(s). The inverse of a lifetime is called the decay constant λ, so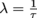
.
In other words, an isotope will start off with a number of particles No and end up with a number N(t) a certain amount of time t later. Mathematically, we can model this relationship with calculus. For now, we'll just write that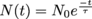
, where t is the amount of time that has passed and τ is the isotope's mean lifetime. We may also write this in terms of the decay constant, 
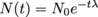. Yet another way we can write this equation is by getting rid of the exponent and change it to a base of 2, and the decay constant morphs into the half-life, with 
.
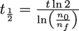The half-life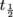
of a nucleus is the time a nucleus takes to decay into another while keeping half of its original amount. By this we mean that if a nucleus starts with an amount No, then at the end of its half-life we'll be left with 
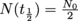. As a function of time, 
.
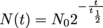A radioactive particle also has an activity or decay rate, which is the number of decays per time unit, such as decays per second, where one decay per second is also called a disintegration per second. One decay per sec is one Becquerel, Bq for short.
In terms of the decay constant, the activity A is given by A = λN, where N is the number of radioactive particles.
We're surrounded by naturally radioactive elements. While its certainly true that the most abundant isotopes of elements aren't radioactive by a strong majority, there are still plenty of radioactive elements around, and most of those have long half-lives so they last longer, though their decay rate is slower per atom.
Three naturally occurring isotopes are Uranium-238, Thorium-232 and Potassium-40. Potassium-40 is commonly absorbed by vegetation and makes its way into a lot of foods we eat, including bananas, seaweed, lima beans and carrots. That doesn't mean you shouldn't eat your veggies, though. The levels of radiation are low.
The units we use for time in the half-life equation don't matter, however, because the unit of time cancels out within the exponent.
The Nuclear Force
When we talked about the electron held in orbit around the nucleus, we mentioned that electrons were negative and the nucleus was positive. The electric force holds the atom together, the attractive electric force between opposite charges.Here's a puzzler: what holds the nucleus together?
Neutrons are neutral and protons are positively charged. The electric force can't act there. Mathematically, if we insert the neutron's charge into Coulomb's Law, we'll get a big fat zero. We have to consider the mutual repulsions of all the protons together in the nucleus for any Z > 1, as well.
"Mutual repulsion" because like charges repel each other. That means something must be missing here. What's this "nuclear glue" that keeps the nucleus together? Why would neutrons hang out with repulsive protons, anyway?
With James Chadwick's 1932 discovery of the neutron came another new concept: the nuclear force. It's a strong force that acts within the range of the nucleus, go figure. Since nucleons reside inside the nucleus, all nucleons feel the presence of the nuclear force.
Let's take a step back. Let's talk about forces. Charged particles, such as protons and electrons, feel the electromagnetic force. Nucleons, such as neutrons and protons, feel the nuclear force. And every particle in the universe feels the gravitational force. It's the relative strength of these forces at various distances that determine which force rules in a given situation. Gravity rules the movement of galaxies and solar systems, the electromagnetic force rules for electrons around a nucleus (and elsewhere), but the nuclear force rules the nucleus.
By continued scattering experiments, the size of the nucleus of an atom was determined to be roughly R = RoA1/3, where Ro = 1.2 fm, that's 1.2 × 10-15 m, and A is the mass number of the nucleus. This image of the Helium atom below gives us a good idea of the size of a nucleus in comparison with the size of an atom. The atom has much more empty space in it than scientists had originally conceived.
The word nucleus comes from Latin. It's short for nux, latin for kernel. Yep, eating popcorn at the movies has an entirely new meaning now, doesn't it?
The nuclear force is actually divided into two. We won't really get into the technical details here, but some particles only feel one kind or the other depending on their nature. These two sides of the nuclear force are called the strong force and the weak force. As its name implies, the weak force is weaker than the strong force. It's also weaker than the electromagnetic force, but still stronger than gravity.
The particles subject to the strong force are called hadrons and the particles that feel the weak force are called leptons. Both protons and neutrons are hadrons. Electrons, incidentally, are leptons, but they're not in the nucleus under ordinary circumstances so in a nuclear sense, we ignore the weak force.
If we inspect the ratio of protons to neutrons throughout the periodic table, we'll notice that the ratio changes.
The smaller atoms have about an equal number of protons and neutrons. Oxygen-16, for instance, has 8 protons, 8 neutrons. When we get to Scandium-45 , however, there appears to be a bit of a branch-off. Scandium has 21 protons, but 24 neutrons. This difference just keeps getting bigger as the sizes of nuclei grow. Why is that? To understand the answer to this question, let's first investigate the binding energy within a nucleus as a function of atomic mass A.
Although we won't discuss nuclear orbitals today (they're waaaay too complicated), just like electrons, nucleons have a binding energy that keeps them in the nucleus. The mass number is the mass of the nucleus. That nucleus contains neutrons and protons, and the binding energy, Eb, that binds them together. The graph above shows that Iron-56 has the highest binding energy per nucleon, granting it the most stable nucleus of all the elements and isotopes out there.
Albert Einstein showed that E = mc2 as we studied in Relativity. Let's apply this to the energy of a nucleus to find the binding energy within the nucleus, Eb.
In that case the total energy in there is E(nucleus) + Eb = E(neutrons) + E(protons). Solving for Eb, we get Eb = E(neutrons) + E(protons) − E(nucleus). Using E = mc2, and dividing out c2, we're left with mass only, such that M(binding) = M(neutrons) + M(protons) − M(nucleus).
The M(binding) here is just the mass associated with the mass energy, otherwise known as the mass defect, or how much the mass changes from E = mc2.
Isotopes
The place where nuclear binding or lack of binding is most evident is in unusually heavy or light isotopes. Add enough neutrons to a nucleus, and it becomes unstable. Take enough neutrons out of a nucleus and it becomes unstable too. Nature may abhor a vacuum, but nuclei abhor instability.Let's review.
The atomic number is the number of protons, Z; the mass number is the number of nucleons, A. This means the number of neutrons N is simply given by N = A − Z. M(neutrons) is just the number of neutrons multiplied by the mass of 1 neutron, and
M(protons) is just the number of protons multiplied by the mass of 1 proton. Review's done; we're moving on.
Let's take
There are two reasons why Mr. Sixteen is so important. The first reason is pretty straightforward. It's the most naturally abundant on the planet, at 99.6% of all the naturally-occurring Oxygen on Earth. If we took a sample of 1000 random Oxygen atoms, we'd get about 996 Oxygen-16 atoms.
There's one more reason, related to the first. Oxygen-16, Oxygen-17, and Oxygen-18, are stable isotopes. This means they will stay as is, not emitting radiation to turn into something else like an unstable isotope would.
Stable isotopes are naturally abundant for a reason: they don't change into something else. So of course unstable isotopes of any element aren't naturally abundant: the nucleus is too prone to change for that to happen.
Radiation
When a substance, compound, or element emits radiation spontaneously in the form of energetic particles or photons, we call that substance, compound, or element radioactive.Radioactivity was discovered by Henri Becquerel in 1896. One day, he noticed that the some photographic film he developed turned out foggy. When he looked into what happened to the film, he realized that the film had been left besides some uranium compounds. He figured the "fogginess" was due to something the uranium was emitting. He was spot on.
We've mentioned radiation before when we studied electromagnetism. Cherenkov radiation and Bremsstrahlung radiation, for instance, are examples of radiation emitted as photons, or light.
The Polish doctoral student Marie Curie followed Beckerel's footsteps with her husband Pierre. Together, Marie and Pierre discovered other radioactive substances. They discovered Thorium, Radium, and Polonium, which Marie Curie named after her native country, Poland. The Curies won the Nobel Prize in 1903 with Becquerel.
The Curie couple discovered three types of emissions: alpha, beta, and gamma radiation. In other words, an unstable isotope spontaneously decays into another element while emitting one (or more) of those three particles from its nucleus. We've encountered α-particles before: they're what Rutherford used in his experiment that led to the discovery of the nucleus.
Once again, alpha particles are Helium nuclei with 2 neutrons and 2 protons. Since there are no electrons in nuclei, an α-particle carries a net +2 charge. The beta particles in β-radiation, on the hand, are electrons. Both α and β particles belong to a class of corpuscular radiation because they have mass, although α-particles, being heavier than electrons, don't travel very far through a material before they lose energy from collisions and stop.
The most powerful and potentially harmful source of radiation comes from gamma-rays, γ-rays. These are photons of the highest energies and frequencies possible in the electromagnetic spectrum, above 100 keV. We also call them "penetrating radiation" because gamma radiation, unlike alpha and beta radiation, can travel through skin. x-rays are penetrating radiation too (there'd be no picture of bones if the x-rays didn't penetrate), which also makes them dangerous.
through.
Any kind of radiation is bad for organisms, as we've all heard by now. Crossing paths with alpha, beta, and gamma radiation causes damage to tissue. Frequent, repeated exposure can lead to cell mutation, which turns into cancer. And that is why we always wear sunscreen, that's right, even the lower energy radiation from the sun's ultraviolet light over time can cause cancer. Radiation is what makes atomic weapons so terrible. It's not just the impact of the explosion itself that cause horrors, but the awful side-effects of alpha, beta, and especially gamma radiation too.
At what rate is this nefarious radiation emitted?
It depends on the isotope and how much of the isotope there is. Each isotope has a mean lifetime τ, pronounced tau. It's the average time a radioactive particle lives before it decays into something else emitting a type of radioactive particle(s). The inverse of a lifetime is called the decay constant λ, so
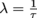.In other words, an isotope will start off with a number of particles No and end up with a number N(t) a certain amount of time t later. Mathematically, we can model this relationship with calculus. For now, we'll just write that
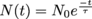, where t is the amount of time that has passed and τ is the isotope's mean lifetime. We may also write this in terms of the decay constant, 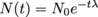. Yet another way we can write this equation is by getting rid of the exponent and change it to a base of 2, and the decay constant morphs into the half-life, with 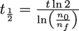.The half-life
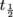of a nucleus is the time a nucleus takes to decay into another while keeping half of its original amount. By this we mean that if a nucleus starts with an amount No, then at the end of its half-life we'll be left with 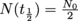. As a function of time, 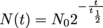.A radioactive particle also has an activity or decay rate, which is the number of decays per time unit, such as decays per second, where one decay per second is also called a disintegration per second. One decay per sec is one Becquerel, Bq for short.
In terms of the decay constant, the activity A is given by A = λN, where N is the number of radioactive particles.
We're surrounded by naturally radioactive elements. While its certainly true that the most abundant isotopes of elements aren't radioactive by a strong majority, there are still plenty of radioactive elements around, and most of those have long half-lives so they last longer, though their decay rate is slower per atom.
Three naturally occurring isotopes are Uranium-238, Thorium-232 and Potassium-40. Potassium-40 is commonly absorbed by vegetation and makes its way into a lot of foods we eat, including bananas, seaweed, lima beans and carrots. That doesn't mean you shouldn't eat your veggies, though. The levels of radiation are low.
Common Mistakes
SI units matter a lot for electron energy level conversion, but not for comparing energy levels to each other.The units we use for time in the half-life equation don't matter, however, because the unit of time cancels out within the exponent.