The first thing we do is look for "bad" values. The "bad" values for this equation are x = -1, which makes the left-hand side of the equation undefined, and x = 2, which makes the right-hand side undefined. These values are definitely from the wrong side of town. Now we go ahead and solve. Way 1: Eliminate denominators. Multiply both sides of the equation by (x + 1) and (x + 2) to find: 3x(x – 2) = x(x + 1) This simplifies to: 3x2 – 6x = x2 + x Then we can rearrange the whole kit 'n' caboodle: 2x2 – 7x = 0 Now we have a polynomial equation, and we know what to do. First, factor: x(2x – 7) = 0 From the factored form we can see that the solutions to the equation are x = 0 and 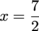 (the solution (the solution 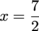 comes from solving the equation 2x – 7 = 0). Before writing down our final answers, we need to make sure 0 and comes from solving the equation 2x – 7 = 0). Before writing down our final answers, we need to make sure 0 and  aren't "bad" values. We should also make sure that they're not seeing each other, so we can be assured they're not having a "bad" romance. aren't "bad" values. We should also make sure that they're not seeing each other, so we can be assured they're not having a "bad" romance. Our two solutions are not, in fact, "bad" answers, so our final answers are: x = 0, 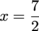 Way 2: Put the fractions over a common denominator. We multiply the left-hand side of the original equation by  and the right-hand side of the original equation by and the right-hand side of the original equation by  . This gives us an equivalent equation: . This gives us an equivalent equation: 
Since the denominators are the same, we compare numerators, which means we need to solve this equation: 3x(x – 2) = x(x + 1) We'll use the same way that we did in Way 1. No way! Yes way. We know that we'll find the same solutions to the equation, which is lovely. |