Whenever we do an experiment like flipping a coin or rolling a die, we get an outcome. For example, if we flip a coin we get an outcome of heads or tails, and if we roll a die we get an outcome of 1, 2, 3, 4, 5, or 6. Unless we're rolling a 20-sided die, in which case we're likely playing Dungeons & Dragons, and the outcome is that we won't go on a date for a few years yet. Ouch.
We call the set of all possible outcomes of an experiment the sample space. The sample space for the experiment of flipping a coin is
{heads, tails}
and the sample space for the experiment of rolling a die is
{1, 2, 3, 4, 5, 6}.
An event is a set of outcomes. The event of rolling an even number with a die is the set
{2, 4, 6}.
If you were looking for odd numbers, it wouldn't be called an "oddent." Still called an "event." Sorry if that's confusing.
Each of the outcomes in this set is an even number, so if we get any of the outcomes in this set we have successfully rolled an even number. Come on...cat's eyes!
An experiment is called random or fair if any outcome is equally likely. Unlike the grand experiment that is life, which is both random and not fair.
If we flip a fair coin, it means either heads or tails is equally likely. No weighted coins allowed, Mr. Trickster Man. If we draw a card at random from a deck, it means any one of the 52 cards (assuming no jokers) is equally likely to be drawn.
When we talk about finding probabilities, we mean finding the likelihood of events. They're different than the skills certain aliens possess, which are generally referred to as "probe abilities." Important distinction.
If an experiment is random/fair, the probability of an event is the number of favorable outcomes divided by the total number of possible outcomes:
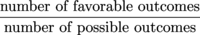
A favorable outcome is any outcome in the event whose probability you're finding (remember, an event is a set).
Sample Problem
If you roll a standard 6-sided die, assuming each side is equally likely to land upwards, the probability of rolling a 1 is
 .
.
Sample Problem
What's the probability of rolling an even number on a 6-sided die?
If you're finding the probability of the event of rolling an even number, any even number is considered a favorable outcome. Especially if it means you can move ahead four spaces and buy Boardwalk.
The probability of rolling an even number on a standard 6-sided die is
 .
.
Since there are 3 ways to roll an even number on a standard die, the probability of rolling an even number is
 .
.
This makes intuitive sense, since half the numbers on a die are even, and half are odd. Although we can't be entirely sure that's true, as we've never been able to look at all six sides at once, and we're always suspicious they keep changing on us when we aren't looking. Okay, so maybe we're paranoid.
Example 1
If you flip a fair coin, what is the probability of getting heads? |
Example 2
A drawer contains 4 blue socks and 6 red socks. If you pull out a sock at random, what is the probability of
|
Exercise 1
Determine the sample space for the following experiment:
Choosing one of the four possible aces from a standard deck of cards.
Exercise 2
Determine the sample space for the following experiment:
Choosing a club from a standard deck of cards.
Exercise 3
Determine the sample space for the following experiment:
Flipping two coins at the same time.
Exercise 4
Write the set for the following event:
Rolling an odd number on a standard 6-sided die.
Exercise 5
Write the set for the following event:
Getting heads on a coin flip.
Exercise 6
Write the set for the following event:
Getting exactly one head after flipping two coins.
Exercise 7
How many possible outcomes are there for the experiment of choosing rock, paper, or scissors at random?
Exercise 8
How many possible outcomes are there for the experiment of choosing a color of the rainbow at random? What is the sample space?
Exercise 9
What is the probability of rolling a 5 with a fair die?
Exercise 10
What is the probability of rolling either 1 or 2 with a fair die?
Exercise 11
What is the probability of drawing the ace of spades at random from a deck of cards (no jokers)? The one in your sleeve doesn't count.
Exercise 12
What is the probability of drawing a king at random from a deck of cards (no jokers)? The one in your right pant leg doesn't count.
Exercise 13
What is the probability of drawing a king at random from a deck of cards (with 2 jokers included)?
Exercise 14
What is the probability of landing at least one tail with two fair coin flips?
Exercise 15
What is the probability of landing exactly two heads with three fair coin flips?

 .
.








