Completing the square always works when solving a quadratic equation, but it's almost always a pain in the butt to actually do. We want a method that's faster and easier to use while being just as reliable.

What we want is the quadratic formula. Here it is, in all its glory (when ax2 + bx + c = 0):

You'll want to memorize this handy little formula. Luckily, it's pretty distinctive. It is possible to derive the formula from scratch, though it requires completing the square (natch). You can see the derivation here, if you like.
Sample Problem
Solve the quadratic equation 2x2 – 5x – 3 = 0 using the quadratic formula.
We recognize this problem. We did this in the last section—there were all kinds of fractions, and it was nasty to work through. Let's see how it goes with the quadratic formula. To start, we note that a = 2, b = -5, and c = -3. We then set up the equation:
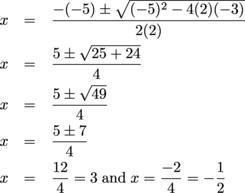
Sample Problem
Solve the equation 2x2 + 2x + 5 = 0 using the quadratic formula.
Using the quadratic formula is pretty mindless once you know the formula. Just plug and chug and plug and chug and choo choo. Sorry, we got carried away.

That's right, rolling along like a train. Next we check our answers.

One down, one to go.

Excellent. Now we pull into the station.
Example 1
Use the quadratic formula to find the roots of y = 2x2 + 4x + 1. |
Example 2
Use the quadratic formula to find the roots of y = x2 – 16. |
Example 3
Use the quadratic formula to find the roots of y = x2 + 4x + 4. |
Example 4
Use the quadratic formula to find the roots of |
Exercise 1
Use the quadratic formula to find the roots of y = -x2 + 5x – 2.
Exercise 2
Use the quadratic formula to find the roots of y = x2 – 3x – 8.
Exercise 3
Use the quadratic formula to find the roots of y = -4x2 + x – 3.
Exercise 4
Use the quadratic formula to find the roots of y = x2 + 3x.
Exercise 5
Use the quadratic formula to find the roots of  .
.






 .
.









