You spin us right round, baby, right round, but not quite like a record, baby. Think flatter. Squatter. More squashed. That's because we're dealing with ellipses.

Unlike a parabola, ellipses are closed shapes. They swing back around to where they started, instead of continuing on and on forever. The trip around seems pretty redundant. But do it with a Formula 1 race car and we've got some great entertainment.
While ellipses have a directrix and focus (actually, they have two of each of them) we don't care too much about them for ellipses. Go, shoo, get out of here. We'll still find the foci—that's the plural of focus—but they aren't the most important parts of an ellipse for us.

The real action for an ellipse is at its axes. It has two of them: a major axis and a minor axis. There's nothing wrong with being a minor, but the major axis is the bigger deal here. Or maybe we should say the longer deal. The axes start and end on the vertices, the farthest two points on each side of the ellipse. They also pass through the center, giving each other a perpendicular "How do you do?" as they pass.
Example 1
Find the center, vertices, and foci of |
Example 2
Find the center, vertices, and foci of |
Example 3
Find the equation of the ellipse with vertices at (-3, 4) and (5, 4), and foci at (-1, 4) and (3, 4). |
Exercise 1
Find the center, vertices, and foci of  .
.
Exercise 2
Find the center, vertices, and foci of 9(x – 3)2 + 4(y + 5)2 = 36.
Exercise 3
Find the center, vertices, and foci of  .
.
Exercise 4
Find the equation of the ellipse with vertices at (4, -5), (4, 5), (1, 0), (7, 0).
Exercise 5
Find the equation of the ellipse with a vertex at (3, 0), a focus at (0, 0), and the center at (2, 0).
 .
. .
.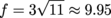
 .
.



