ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Solving Equations Videos 8 videos
ACT Math Section: Elementary Algebra Drill 2, Problem 5. Use these two equations to solve for both x and y.
ACT Math Section: Elementary Algebra Drill 3, Problem 3. Solve for x.
ACT Math Intermediate Algebra Drill 2, Problem 5. Solve for x in this inequality.
ACT Math 1.5 Elementary Algebra 264 Views
Share It!
Description:
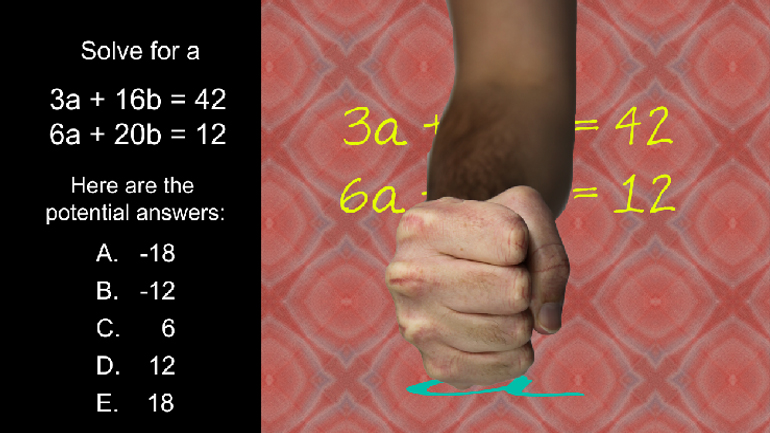
Math Elementary Algebra: Drill 1, Problem 5. Solve for a using substitution.
- Elementary Algebra / Substitution
- Elementary Algebra / Linear equations
- Product Type / ACT Math
- Foreign Language / Arabic Subtitled
- Foreign Language / Spanish Subtitled
- Foreign Language / Korean Subtitled
- Foreign Language / Chinese Subtitled
- Elementary Algebra / Evaluation of algebraic expressions through substitution
Transcript
- 00:03
Here's your shmoop de jour
- 00:06
Solve for a using substitution: 4a = b - 8
- 00:10
a + b = 18
- 00:13
And here are the potential answers...
- 00:17
OK fun problem.
Full Transcript
- 00:19
It's another one of those problems that wants us to put our super-duper substitution skills
- 00:25
to work.
- 00:28
We want to get either a or b alone. Like what is a simply or what is b simply
- 00:36
In the first equation, b's already by itself...
- 00:39
...so we can just add 8 to both sides to get b = 4a + 8.
- 00:48
Plugging that into the other equation in place of b, we get a + 4a + 8 = 18...
- 00:54
...and when we slap our a terms together and subtract 8 from each side...
- 00:58
...we're left with 5a = 10. Divide both sides by 5, and a = 2.
- 01:04
Our answer is B.
- 01:05
As in, "Binomial Man."
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
You don't want to leave a bunch of unsolved rational equations sitting around.
Solving inequalities using blob fish? Yes, please!