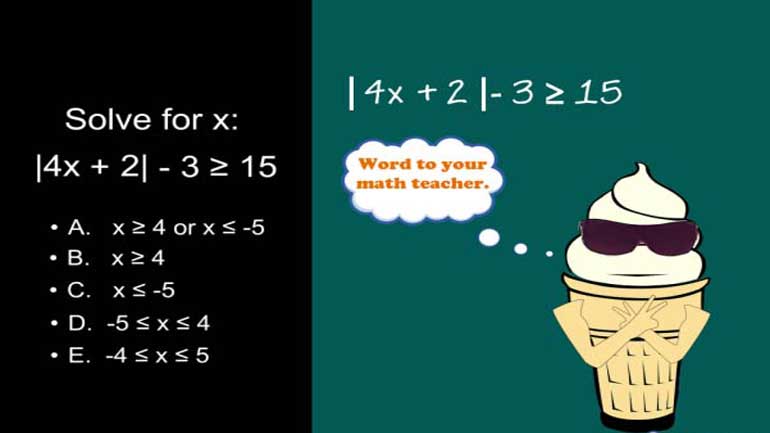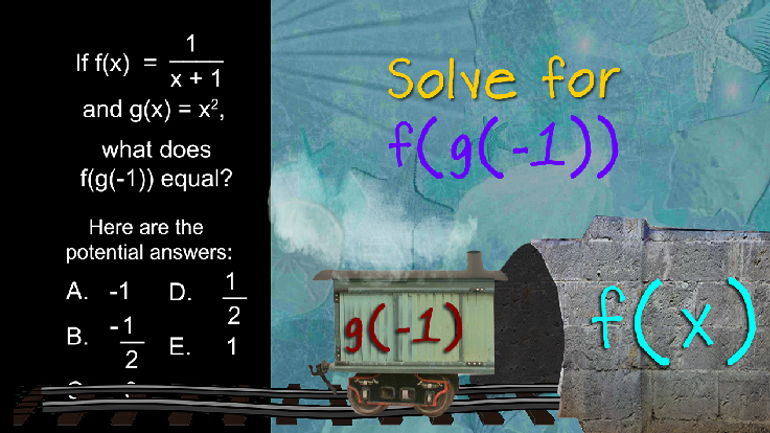ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Playlist ACT® Intermediate Algebra 25 videos
ACT Math Intermediate Algebra Drill 1, Problem 1. What is the product of (a – 3)2?
ACT Math Intermediate Algebra Drill 1, Problem 2. Find the product of (2a + 6)2.
ACT Math Intermediate Algebra Drill 1, Problem 3. Can you find the value of a in this expression?
ACT Math 2.4 Intermediate Algebra 384 Views
Share It!
Description:
ACT Math Intermediate Algebra: Drill 2, Problem 4. Solve for x.
Transcript
- 00:02
Here's your shmoop du jour...
- 00:05
Solve for x: the absolute value of 4x plus
- 00:08
2... minus 3... is greater than or equal to 15.
- 00:14
And here are the potential answers...
- 00:18
OK so what is this question asking?
Full Transcript
- 00:20
It's a pretty vanilla absolute value question.
- 00:24
We can ignore the vertical lines for a moment...so we have 4x plus 2 minus 3 is greater than
- 00:30
or equal to 15... or 4x minus 1 is greater than or equal to 15.
- 00:36
Then... 4x is greater than or equal to 16... so x is greater than or equal to 4.
- 00:44
Again, that's only if we ignore the absolute value lines.
- 00:49
So now let's max out what we can do if we color... inside the lines.
- 00:53
We're going to worry about the absolute value of 4x plus 2 being greater than or equal to 18...
- 01:00
...so... think about what x value could make 4x plus 2 NEGATIVE 18; we'll then take the
- 01:07
absolute value of that to make it GREATER than 18.
- 01:10
That is, what NEGATIVE values of x would do this for us?
- 01:14
Well, negative 1, 2 and 3 and 4 don't help us much, but negative 5 gets us there because
- 01:20
we have 4 times negative 5, which is negative 20...
- 01:24
... then add 2, and we have negative 18, but when we take the absolute value of it we're there.
- 01:35
So the range that x can take to satisfy this equation is that it lives somewhere between
- 01:39
negative 5 and positive 4...
- 01:41
...Answer: A.
- 01:43
And that's why you always have to be careful to... stay inside the lines.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
You don't want to leave a bunch of unsolved rational equations sitting around.
Solving inequalities using blob fish? Yes, please!