ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Systems of Equations Videos 73 videos
How do you solve a system of linear inequalities? Aw, man...and we thought solving a problem like Maria was tough...
Please note: If starting your own petting zoo, Shmoop recommends you stock it with animals that aren’t quite so likely to bite your hand off. Tha...
ACT Math 3.5 Intermediate Algebra 292 Views
Share It!
Description:
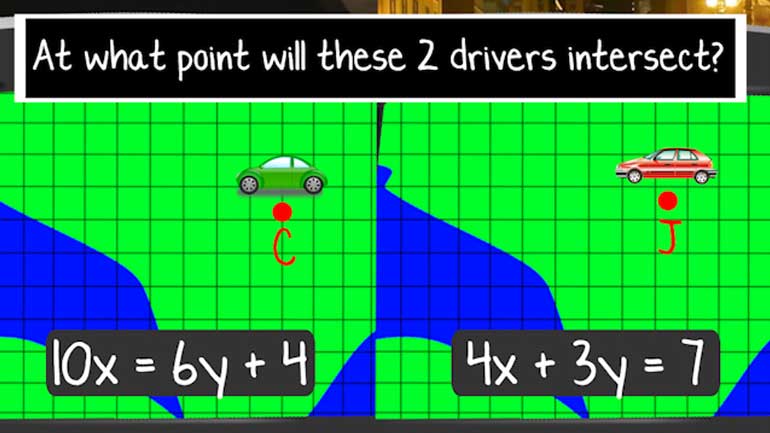
ACT Math Intermediate Algebra Drill 3, Problem 5. Solve this system.
Transcript
- 00:02
Here's your shmoop du jour, extra crackers included...
- 00:07
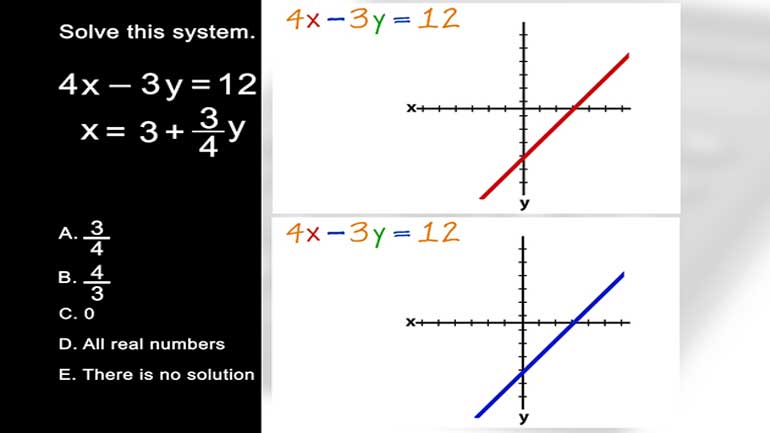
Solve this system: 3x - y = 2 6x - 2y = 5
- 00:13
And here are the potential answers...
- 00:17
OK so whenever we're given two equations and
- 00:20
are told to solve the system, we're actually trying to solve for the point of intersection
Full Transcript
- 00:25
of the two equations.
- 00:27
Elimination is one method of solving equations, so let's try that first.
- 00:32
Multiply the first equation by 2... and we get 6x minus 2y equals 4.
- 00:40
But wait... that looks almost exactly the second equation, except the 4 isn't a 5.
- 00:45
What does that mean?
- 00:46
Well, whenever we see that two equations in standard form have the same coefficients in
- 00:56
front of their variables, we know that these two lines are parallel.
- 01:01
If two lines are parallel, they have no point of intersection... so there is no solution
- 01:05
for this problem.
- 01:06
Looks like E's our answer.
- 01:09
Drive safe, and watch those points of intersection, everyone.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...