ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Playlist ACT® Plane Geometry 25 videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Plane Geometry Drill 5, Problem 5. How much material do you need to cover the entire tent?
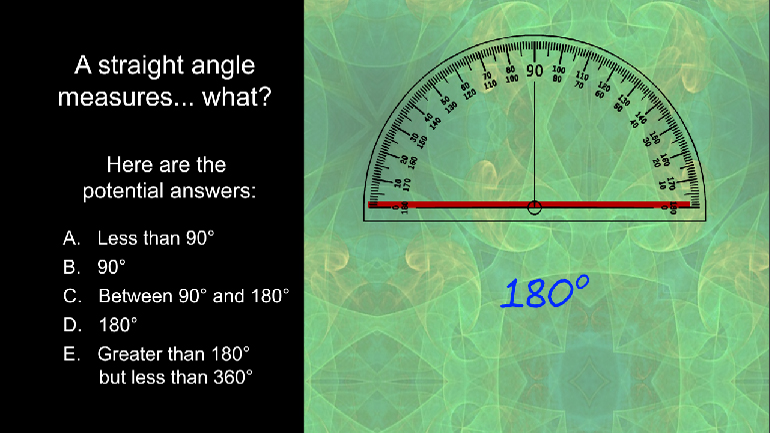
Math Plane Geometry: Drill 1, Problem 1. What does a straight angle measure?
ACT Math 5.5 Plane Geometry 601 Views
Share It!
Description:
ACT Math: Plane Geometry Drill 5, Problem 5. How much material do you need to cover the entire tent?
- Plane Geometry / Area
- Product Type / ACT Math
- Foreign Language / Arabic Subtitled
- Foreign Language / Korean Subtitled
- Foreign Language / Chinese Subtitled
- Foreign Language / Spanish Subtitled
- Geometry / Visualize relationships between two-dimensional and three-dimensional objects
- Properties, Measurement, and Dimension / Visualize relationships between two-dimensional and three-dimensional objects
- Plane Geometry / Applications of geometry to three dimensions
Transcript
- 00:02
Here's your shmoop du jour, brought to you by Outward Bound. Don't worry—we won't
- 00:07
throw you to the wolves.
- 00:09
It is your first day of Outward Bound and you need to pitch a tent in the form of a
- 00:12
triangular prism with the dimensions shown.
- 00:16
How much material do you need to cover the entire tent?
Full Transcript
- 00:20
And here are your potential options...
- 00:25
Since we're trying to find the amount of material needed to cover the tent, we need
- 00:28
to find the surface area.
- 00:30
First, we need to find the area of each individual shape
- 00:33
in the triangular prism and then... add them all up.
- 00:37
Let's start with the triangles that make up the front and back of the tent.
- 00:41
They have a height of 5, and a base length of 24
- 00:44
We can plug in these values to get the area of each triangle, which turns out to be 60
- 00:51
square feet. There are two of these in the tent, so they
- 00:54
have a total surface area of 120 square feet. As for the two remaining rectangles,
- 00:58
we have a length of 40 feet, and a width of 13 feet; by calculating the area of each,
- 01:06
we get 520 square feet. Again, we have two of these, so we have to
- 01:10
multiply it by 2 to get 1040 square feet. We have to add the areas of the triangles
- 01:16
and the rectangles to get our total surface area, and when we do that, we get 1,160 square
- 01:22
feet of material needed. Option D is just right.
Related Videos
ACT Math: Plane Geometry Drill 3, Problem 1. What is the area of the trapezoid shape in the video?
ACT Math: Coordinate Geometry Drill 1, Problem 1. Which inequality is expressed by the number line?
ACT Math: Intermediate Algebra: Drill 3, Problem 1. Find the fifth number in the series.
Haven't you always wondered how much cardboard it takes to encase a trunk warmer for your pet elephant?
Want to figure out the area and perimeter of irregular shapes? Break them down into regular shapes. For example, a flower can be broken down into s...