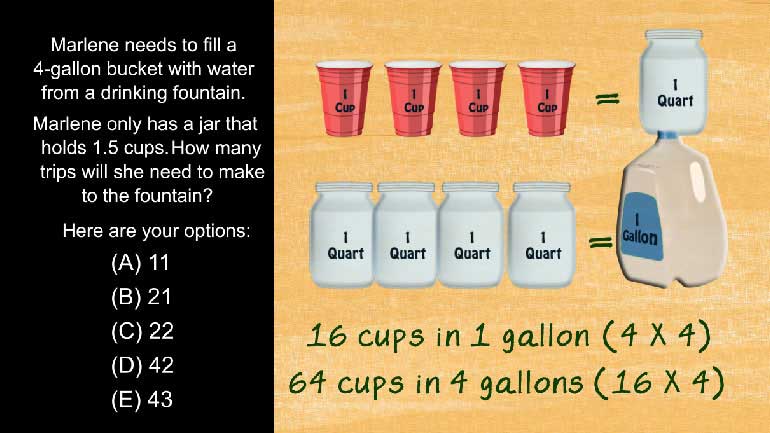ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Appropriate Units and Scales Videos 17 videos
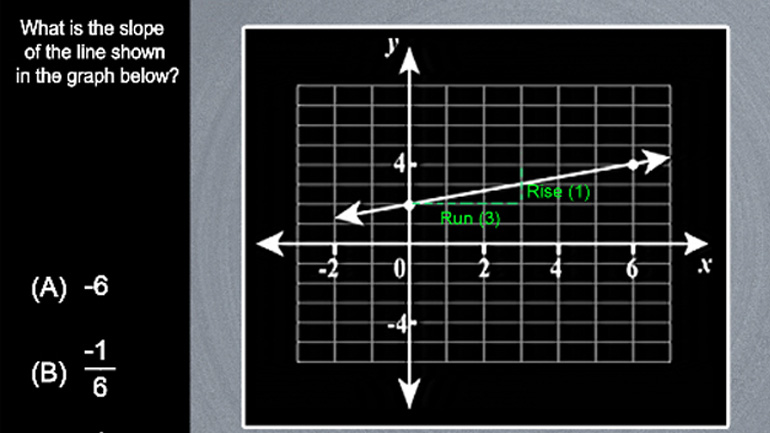
Algebra and Functions: Drill Set 4, Problem 5. What is the slope of the line in the graph?
CAHSEE Math 4.2 Mathematical Reasoning 182 Views
Share It!
Description:
Mathematical Reasoning Drill 4, Problem 2. How many people failed to return the survey?
Transcript
- 00:03
Here’s your shmoop du jour...
- 00:05
A survey was taken of 1,000 randoms to determine people's favorite way of paying for Band-Aids.
- 00:11
The following graph shows the results from the surveys that were returned.
- 00:15
How many people failed to return the survey?
- 00:18
Possibly because they were being held at gunpoint by the Band-Aid Bandits?
Full Transcript
- 00:22
And here are the potential answers…
- 00:26
1000 people in total were given a survey, and all of the responses are shown in the pie chart.
- 00:32
That means that people who didn’t respond aren’t shown.
- 00:35
Since we know the numbers of everyone who did respond…
- 00:37
…if we add those numbers up we can find the total number of respondents.
- 00:41
Then, we can use that to find the total number of people who didn’t return the survey.
- 00:46
Let’s get started on the first step, finding the total number of people who successfully
- 00:50
returned the survey. Thank you very much.
- 00:52
We can do this by summing the numbers in each section of the pie chart.
- 00:56
This comes out to 190 + 170 + 140 + 80 + 60, which is 640.
- 01:02
If there were six hundred forty people who did respond, that means the rest of the thousand
- 01:08
failed to respond. So, we can just subtract 640 from 1,000 to get 360.
- 01:14
The answer is (B).
- 01:15
As in… “Band-Aid Bandits.”
Related Videos
CAHSEE Math: Algebra and Functions Drill 5, Problem 3. Solve the equation.
The video will show you how to plot points in 3D using the axes of the 3D coordinate system. Make sure you're wearing your special glasses for this...
When graphing inequalities, you graph the line, shade the corresponding side, and plug in the point. The end!
One formula to rule them all, one formula to find them. One formula to bring them all, and in the darkness bind them. Or something like that. I...