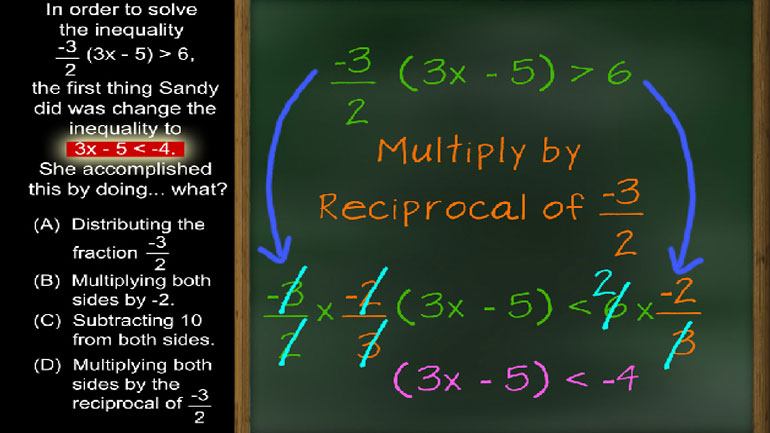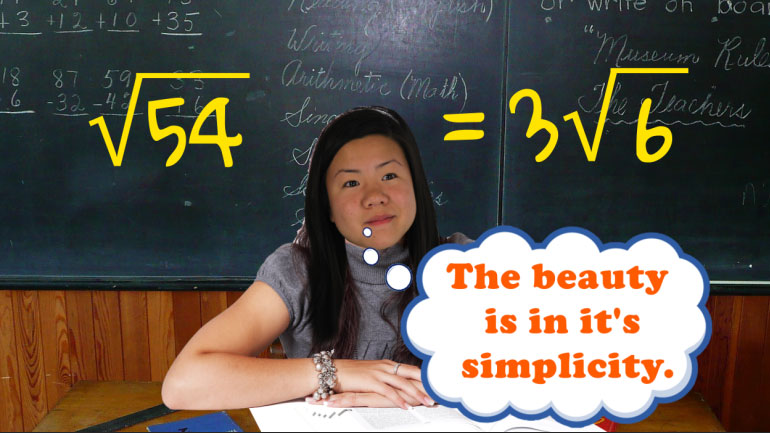ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Algebra I Videos 30 videos
CAHSEE Algebra I: Drill 1, Problem 1. What are some of the properties used to solve this equation?
CAHSEE Math Algebra I: Drill 1, Problem 2. Find the negative reciprocal.
CAHSEE Math 6.4 Algebra I 185 Views
Share It!
Description:
CAHSEE Math Algebra I: Drill 6, Problem 4. How much more ground can the Batmobile cover traveling at a speed of 75 mph in the same amount of time?
Transcript
- 00:03
Here’s a shmoopy question for ya…
- 00:05
Batman totally forgot he was supposed to be back in Gotham for a… business meeting in about an hour.
- 00:10
The Batmobile, traveling at an average of 60 mph, took a certain amount of time to cover
- 00:15
a distance of 80 miles.
- 00:17
How much more ground can it cover traveling at a speed of 75 mph in the same amount of time?
Full Transcript
- 00:23
Here are the potential answers…
- 00:28
So… what is this question asking?
- 00:30
It’s a distance, rate and time problem which we have to just think through.
- 00:34
First, let’s put everything in the same units.
- 00:37
In this problem, we’re all miles… Batman wouldn’t dare fool around with kilometers.
- 00:41
That’s Alfred’s thing.
- 00:43
The Batmobile was going 60 miles an hour, so it can travel, well… 60 miles
- 00:47
in one hour… or 1 mile per minute.
- 00:49
So if it goes 80 miles, then it’s travelled 80 minutes.
- 00:53
But the key thing to glean here is that the Batmobile went for 80 minutes… or an hour
- 00:57
and 20 minutes… or 1.33 hours.
- 01:02
So now what if the Batmobile didn’t hit much traffic and was instead going 75 miles an hour?
- 01:07
To figure out how far it would have driven in that same amount of time, we multiply its
- 01:11
rate of 75 mph by 1.33 and we get… about 100 miles.
- 01:16
So the DIFFERENCE between the two distances is 20 miles.
- 01:22
Answer A. As in, "Alfred."
Related Videos
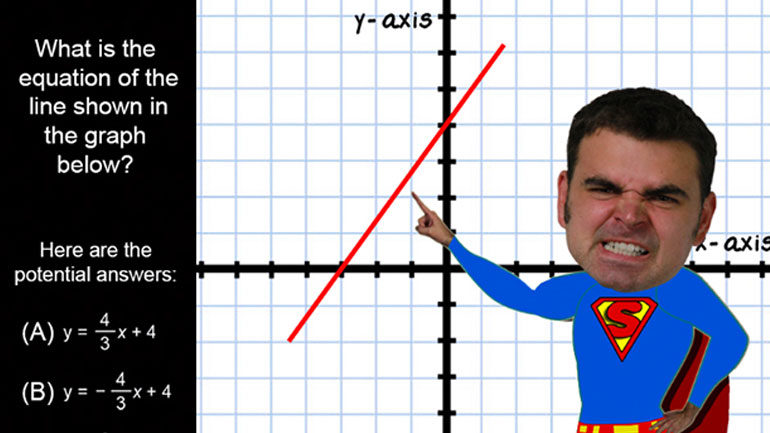
CAHSEE Math: Algebra and Functions Drill 5, Problem 3. Solve the equation.
We don't like knocking people down to size, but we do like simplifying radicals. Join us?
If fleeing criminals always fled the scene of the crime at perfect right angles, it would be much easier to determine their whereabouts. Fortunatel...
Okay, so this probably isn't going to help you master Pokemon Go, but game theory can be applied to all sorts of situations. Even stomping your old...