ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
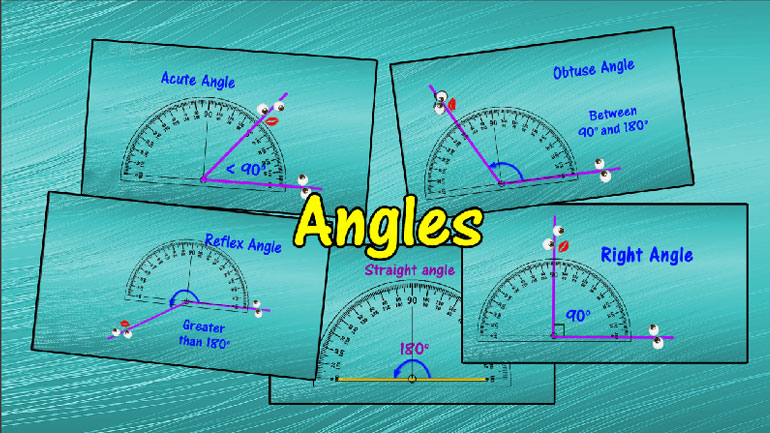
Angles Videos 25 videos
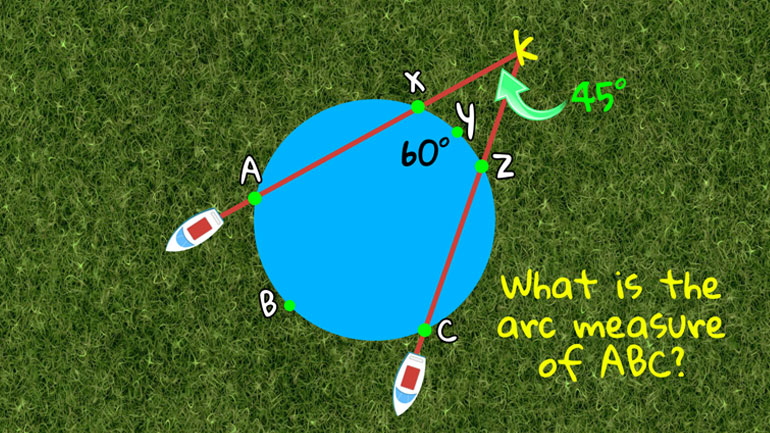
We inscribed some angles on the walls of our office, but our boss got mad, so we made this video instead.
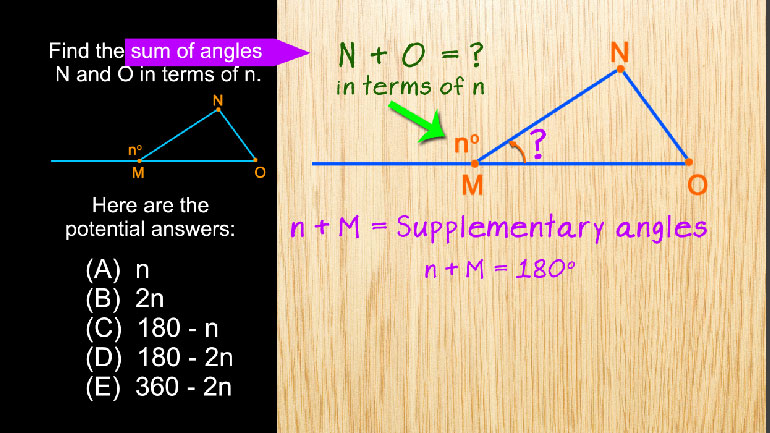
Unlike anything that enters the Bermuda Triangle, Exterior angles can be found—in more than one way. This video covers how to use the remote inte...
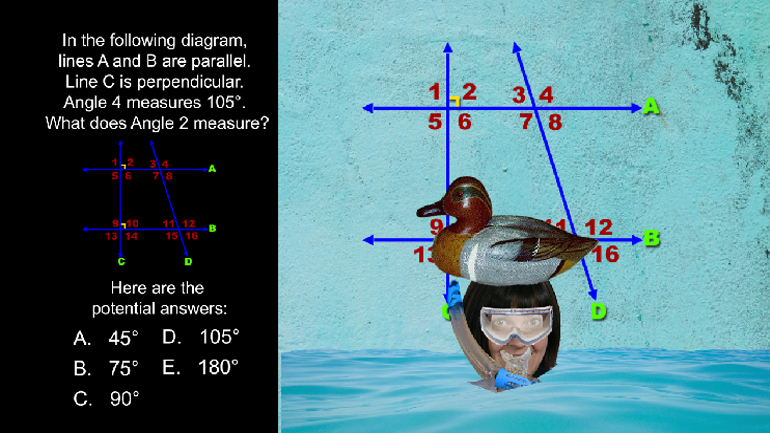
Converting Between Degrees and Radians 1359 Views
Share It!
Description:
If you bake a pie that's 360 degrees...you should probably let it cool down a little. While you're waiting to ingest all those delicious, delicious calories, though, watch this video.
Transcript
- 00:03
converting between degrees and radians a la shmoop
- 00:07
the citizens of Krusty hollow have just finished making the world's largest [Women holding large apple pie]
- 00:12
apple pie unfortunately for them the tempting aroma has attracted the
- 00:16
attention of a handful of giants living on a cloud above them
- 00:20
Tommy, Teddy, Benny, Manny, Gary and Jenny the Giants show up to crash the party [Giants appear]
Full Transcript
- 00:25
and crusty hollow-ites scatter.... to divide the pie evenly Tommy pulls out
- 00:31
his handy-dandy protractor which measures angles in degrees we know that
- 00:36
a circle is 360 degrees if Tommy evenly divides that between he and his five [Circle divided into 5 portions]
- 00:42
friends then each giant gets 1/6 of 360 or 60 degrees of pie... because Giants are
- 00:49
always challenging themselves Tommy wonders if he can convert the
- 00:53
number of degrees in his slice to radians back in giant-high, Tommy learned
- 00:57
that a full circle has two pi radians which is equal to 360 degrees so to
- 01:03
convert from degrees to radians all he has to do is multiply the number of [Conversion of degrees to radians appears]
- 01:06
degrees by pi over 180 remember Tommy slice is 60 degrees so 60 times pi over
- 01:13
180 simplified is the same thing as pi over 3 after gorging themselves on pi 2
- 01:20
of the giants head back into the cloud but right after they leave the remaining [Two giants hop onto cloud and disappear]
- 01:24
Giants discover a second massive pie in the neighboring town of compote hills...
- 01:29
Tommy cuts the pie into 4 even slices each with a measure of pi over 2 radians
- 01:35
then wonders what that would be in degrees well if the number of degrees [Pie divided into 4 sections]
- 01:42
multiplied by pi over 180 gives you the number of radians then what if we flip
- 01:46
the fraction around to get from radians to degrees the formula that Tommy uses
- 01:51
to convert from radians to degrees is the number of radians multiplied by 180
- 01:55
over pi equals number of degrees... so in the equation pi over 2
- 02:00
times 180 over pi the pi in the numerator and the pi in the denominator
- 02:04
cancel out and 180 divided by 2 gives you 90 degrees each slice of pie is pi
- 02:10
over 2 radians or 90 degrees there you go Tommy feels quite satisfied both by [Tommy and giants stood together]
- 02:16
the desert and his formidable algebra skills
Related Videos
Haven't you always wondered how much cardboard it takes to encase a trunk warmer for your pet elephant?
Want to figure out the area and perimeter of irregular shapes? Break them down into regular shapes. For example, a flower can be broken down into s...
It's one thing when all those shapes are sitting flat on the page. But when they start popping out and invading our personal space bubble, we get a...
Does thinking about 3D Geometry get you bent out of shape? Never fear! Watch this video and figure out some fun new shapes to bend back into. We're...
ACT Math: Plane Geometry Drill 3, Problem 5. How long would it take for the wheel to make two rotations?