ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
AP Calculus BC Videos 14 videos
What do snickerdoodles and velocity have in common? Derivatives! No, that wasn't a bad attempt at a joke. Get on our level by watching this speedy...
Riemann sums are a way to estimate the area under a curve. Check out the video for all the deets.
AP Calculus 1.4 Derivatives 202 Views
Share It!
Description:
AP Calculus 1.4 Derivatives. Which of the following best describes the quantity?
Transcript
- 00:00
Thank you We sneak all right Put this problem in
- 00:05
your calculator in shmoop All right Which of the following
- 00:08
best describes the quantity d y t ax given the
- 00:11
relation why cubed minus four x y squared plus eleven
- 00:14
x cubed equals seven and hear the potential All right
Full Transcript
- 00:19
thinking thinking we're doing okay They're asking us to find
- 00:24
the y d x which means this is a derivatives
- 00:27
problem to find the derivative of this relation we typically
- 00:30
right Why explicitly is a function of x so it
- 00:33
looks like why equals something But in this case it's
- 00:37
really hard to isolate Why So we can find the
- 00:39
derivative implicitly Instead this is called implicit differentiation shockingly which
- 00:46
basically means the dependent variable Why has not been written
- 00:50
explicitly in terms of the independent variable x So we
- 00:54
start by applying the derivative with respect to x to
- 00:57
each and every term in the equation Well the first
- 01:00
term is three y squared times d y t ax
- 01:03
because we're finding the derivative of ah wai term with
- 01:06
respect to x All right our second term is negative
- 01:09
for x times Why squared all for this term we
- 01:13
have to use the product rule because we have two
- 01:15
terms multiplied by each other Recalled that the product rule
- 01:18
tells us that the derivative of f of x times
- 01:22
g of ax equals f of x times the derivative
- 01:26
of g of x plus the derivative of f of
- 01:30
x times G of x we can pull out the
- 01:32
minus four as a constant and we'll get x times
- 01:36
two why the y d x plus y squared times
- 01:40
d x d acts which is just one So the
- 01:43
second term simplifies to negative eight X y c y
- 01:47
t ax minus for y squared All right Third term
- 01:51
eleven x cube becomes thirty three x squared We'd multiply
- 01:55
it by d x d x here too But that's
- 01:58
still just one and finally the derivative of seven or
- 02:01
any constant ever is just zero Now it can isolate
- 02:05
the righty axe and move the terms without d y
- 02:08
d x to the other side of the equation Well
- 02:10
the widely axe times three y squared minus eight x
- 02:13
y equals four y squared minus thirty three x squared
- 02:17
Then we just divide by three y squared minus eight
- 02:19
X y to get the idea ax equals four y
- 02:22
squared minus thirty three x squared all over three y
- 02:26
squared minus eight x Y look carefully at the answers
- 02:29
because they all look really similar He is Our answer 00:02:34.0 --> [endTime] is in the river No
Related Videos
AP Calculus: Problem Explanation Limits Drill 1, Problem 1. Which of the following are true about the pictured function?
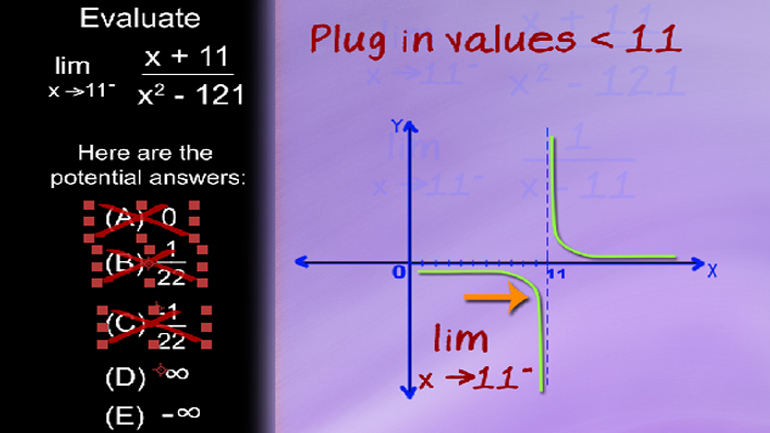
AP Calculus: AB/BC Limits Drill 1, Problem 5. Evaluate the limit.
Breathe in deeply through the nose... Now slowly exhale... Breathe in... And out... Now visualize the graph of the limit of f(x) as x approaches 2....
AP Calculus 1.4 Limits. Given the limit, which of the following are true?
AP Calculus 2.3 Limits. Which of the following facts is helpful in determining the limit?