ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
AP Calculus BC Videos 14 videos
What do snickerdoodles and velocity have in common? Derivatives! No, that wasn't a bad attempt at a joke. Get on our level by watching this speedy...
Riemann sums are a way to estimate the area under a curve. Check out the video for all the deets.
AP Calculus 1.4 Limits 231 Views
Share It!
Description:
AP Calculus 1.4 Limits. Given the limit, which of the following are true?
Transcript
- 00:00
Thank you We sneak here's your shmoop too sure brought
- 00:05
to you by x values which are of course the
- 00:07
values you store in your x files Somebody's listening art
- 00:13
If the limit as x approaches a of half of
- 00:17
acts people's l then which of the following are true
Full Transcript
- 00:21
Okay here the potential answers Ah this is better This
- 00:26
problem is purely conceptual so we won't have to do
- 00:28
any calculations Thank goodness we just need to determine which
- 00:31
combination of the three given statements is true Well if
- 00:36
we remember the definition of a limit we can easily
- 00:38
tell that statements one into our true function on lee
- 00:41
has a limit at a value A both the left
- 00:44
and right limits are the same In other words both
- 00:47
sides of the function have to approach the same values
- 00:50
Respect stand Since if i didn't we wouldn't have a
- 00:53
single limit either way at least we're not limitless Fine
- 00:57
Now that we know the first two statements are true
- 01:00
Will display statement three because we can statement three says
- 01:04
that value at a must be equal to the limit
- 01:07
of the function as x approaches a to disprove this
- 01:10
We just need to think of a case where this
- 01:12
isn't true Well one example where the function f of
- 01:16
x is not continuous at a but has a limit
- 01:20
in this case f of a one point five but
- 01:24
its limit as x approaches a is one They're different
- 01:28
So statement Three False Great Now that we know statement
- 01:31
three falls we can be sure answers The on ly
- 01:34
statements wanted were true you It was certainly a giant 00:01:37.051 --> [endTime] leap for math kind
Related Videos
AP Calculus: Problem Explanation Limits Drill 1, Problem 1. Which of the following are true about the pictured function?
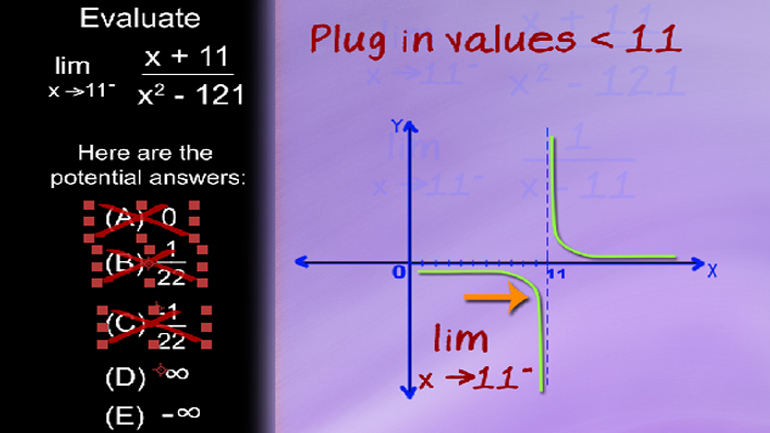
AP Calculus: AB/BC Limits Drill 1, Problem 5. Evaluate the limit.
Breathe in deeply through the nose... Now slowly exhale... Breathe in... And out... Now visualize the graph of the limit of f(x) as x approaches 2....
AP Calculus 2.3 Limits. Which of the following facts is helpful in determining the limit?