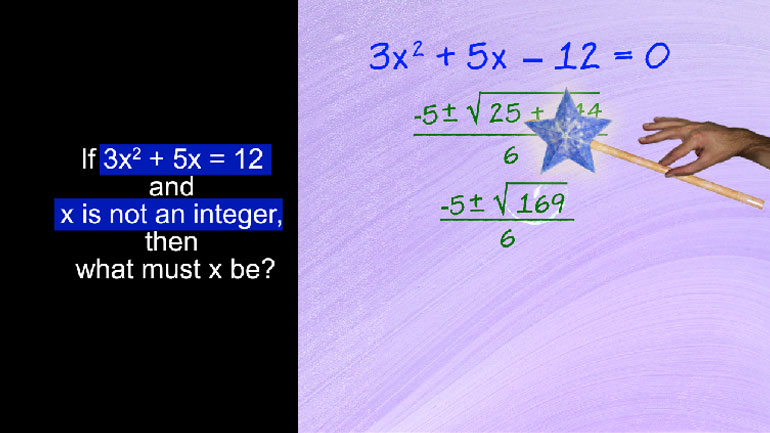ShmoopTube
Where Monty Python meets your 10th grade teacher.
Search Thousands of Shmoop Videos
Statistics and Probability Videos 134 videos
SAT Math: Statistics and Probability Drill 1, Problem 2. If the four largest numbers in the set were doubled, what would happen to the median...
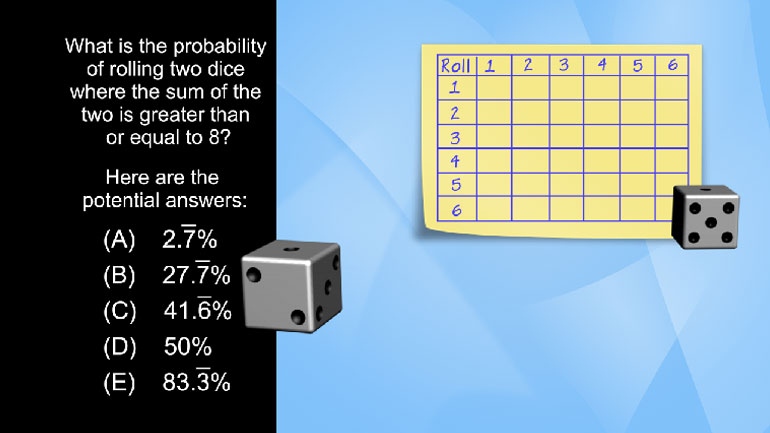
SAT Math 1.4 Statistics and Probability. If two standard 6-sided dice are rolled, what is the probability that the sum of the dice will be gre...
SAT Math 1.5 Statistics and Probability. If Silas draws one card, then places it in his pocket and draws another, what is the probability that...
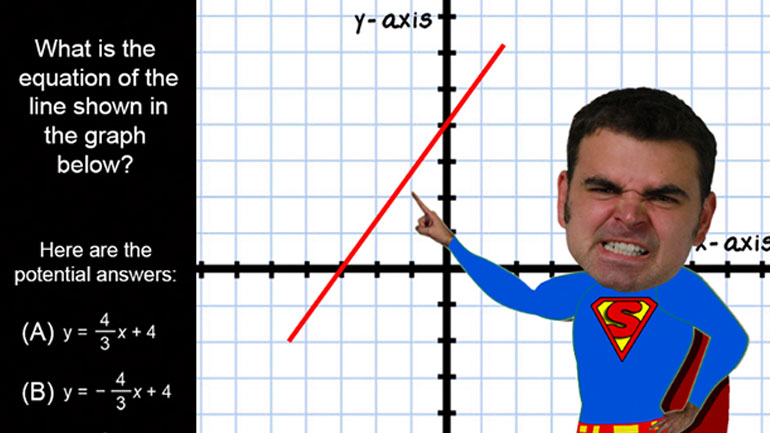
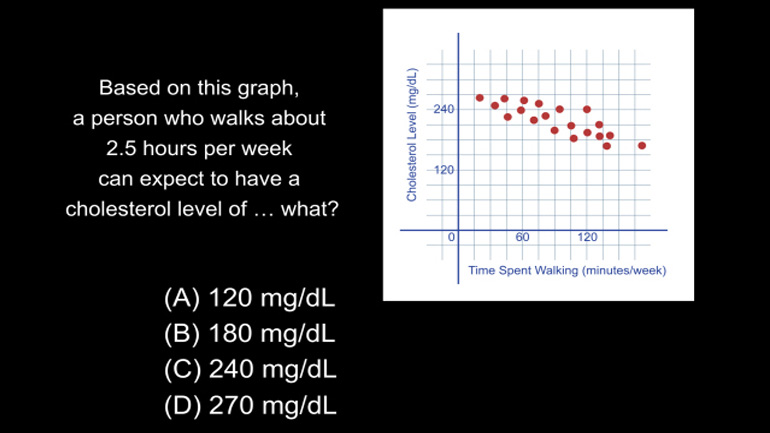
SAT Math 1.2 Statistics and Probability 1060 Views
Share It!
Description:
SAT Math: Statistics and Probability Drill 1, Problem 2. If the four largest numbers in the set were doubled, what would happen to the median value?
Transcript
- 00:03
Here’s your shmoop du jour, brought to you by hypothetical situations.
- 00:07
Well…let’s just suppose that it is…
- 00:11
A data set contains nine numbers.
- 00:13
If the four largest numbers in the set were doubled, what would happen to the median value?
- 00:19
And here are the potential answers…
Full Transcript
- 00:23
Whenever we’re given a hypothetical data set without many details, we can always make up our own values.
- 00:29
For example, in this case, we know our data set has 9 numbers.
- 00:32
So we just need to make up a data set that… works.
- 00:35
The four largest numbers are doubled. That's 9, 8, 7, and 6 in this case. We're gonna double those.
- 00:43
So what happens to the median value?
- 00:46
Remember that the median value is simply the middle value of all of the data.
- 00:52
We can find it by repeatedly getting rid of the minimum and maximum values until we’re
- 00:56
left with one number.
- 00:58
In our first data set, we’d get rid of 1 and 9 first. Then 2 and 8, followed by 3 and 7.
- 01:03
Finally, we get rid of 4 and 6, to be left with 5.
- 01:07
What about our second, altered data set?
- 01:10
First we get rid of 1 and 18, 2 and 16, 3 and 14, and finally 4 and 12.
- 01:14
We’re left with 5.
- 01:16
In both cases, we’re left with 5 as the median.
- 01:19
Our answer is A… the median doesn't change.
Related Videos
SAT Math 2.1 Geometry and Measurement. What is the measure of angle z in terms of x and y?
In 2014, the unemployment rate of one county in California was 7%. In another county, the unemployment rate was 11%. Which of the following express...
Angela is making cookies for a bake sale. She expects each batch of her cookies to sell for $40. It costs her $10 to make one batch of cookies, and...